Encodage de l'information
- Codage des nombres entiers naturels
- Connaître les bases binaire, décimale & héxadécimale
- Passer d'une base à l'autre
- Effectuer des opérations simple dans les différentes bases
- Codage des caractères (normes ASCII et UTF-8)
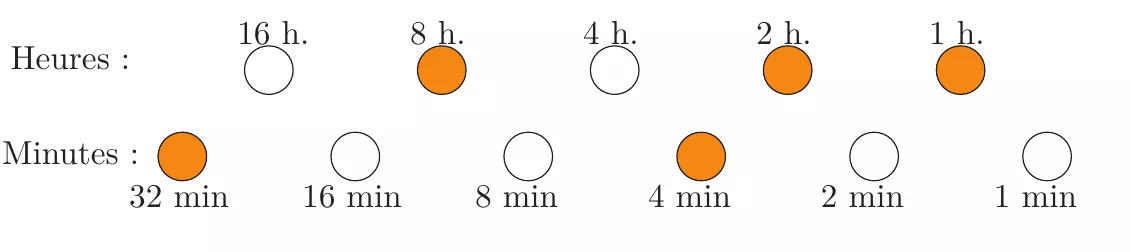
Un horloger excentrique a eu l’idée de fabriquer une montre sur laquelle l’heure est indiquée par 10 diodes électroluminescentes appelées
1) Quelle heure est-il ?
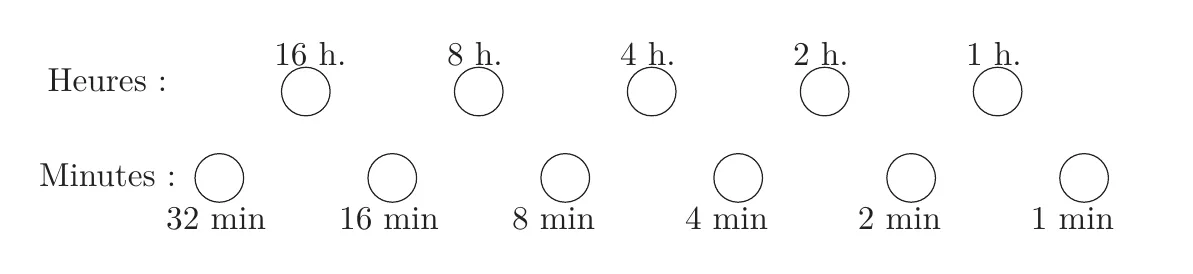
2) Quelle heure est-il ?

Qu'affiche l'horloge quand il est 10h 20 ?
Qu'affiche l'horloge quand il est 21h 43 ?

Quelles sont les élements important de cette horloge ? Trouve une autre représentation pour afficher 21h43.
Pour convertir un mot binaire en nombre décimal, il suffit de multiplier la valeur de chaque bit par son poids, puis d'additionner chaque résultat.
Le mot binaire 1101 vaut en décimal :
Le mot binaire 1101 vaut en décimal :
Le mot binaire 1101 vaut en décimal :
Le mot binaire 1101 vaut en décimal :


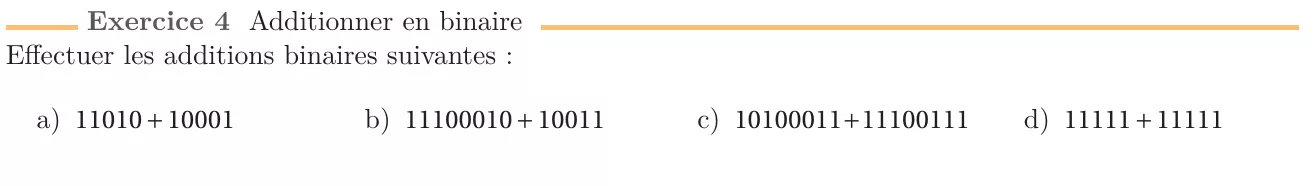
 TP :
Convertisseur
TP :
Convertisseur| Nombre de bits | Valeur maximale | Calcul |
|---|---|---|
| 8 | 255 | 2^8-1 |
| 16 | ... | ... |
| 32 | ... | ... |
| 64 | ... | ... |
| 128 | ... | ... |
| 11010 | 11100010 | ||||
| + | 10001 | + | 10011 |
| 10100011 | 11111 | ||||
| + | 11100111 | + | 11111 |

| Représentation binaire UTF-8 | Signification |
|---|---|
| 0xxxxxxx | 1 octet codant 1 à 7 bits |
| 110xxxxx 10xxxxxx | 2 octets codant 8 à 11 bits |
| 1110xxxx 10xxxxxx 10xxxxxx | 3 octets codant 12 à 16 bits |
| 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx | 4 octets codant 17 à 21 bits |
| Caractère | Numéro du caractère | Codage binaire UTF-8 |
|---|---|---|
| A | 65 | 01000001 |
| é | 233 | 11000011 10101001 |
| € | 8364 | 11100010 10000010 10101100 |
| 𝄞 | 119070 | 11110000 10011101 10000100 10011110 |
| En base 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| En base 16 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| En base 2 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 |
Message du popup !